三平方の定理、立体の体積・表面積 解説 右図のような立体の体積・表面積は,四角錐の高さなどを三平方の定理で求めてから計算します。 右図は底面が1辺の長さ4cmの正方形,側面が1辺の長さ4cmの正三角形です。 体積を求めるには底面積×高さ÷3の公式を2 三平方の定理より正三角形の高さを求める。 s1dp (1a2$)d= 3 底辺×高さ÷2より正三角形の面積を求める。三角形の面積の求め方 正三角形abcが円oに内接していて、 直径bdと辺acの交点をe, adとbcを延長し交点をfとする。 deは1cm このときの三角形abfの面積を求める問題があります。 (点aを上方において、点bを左下、点cを右下として正三角形をとった場合 点dは点c

簡単公式 二等辺三角形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
正三角形 面積 求め方 小学生
正三角形 面積 求め方 小学生-正三角形 (高さから辺と面積)|三角形の計算|計算サイト 指定された正三角形の高さから公式で1辺の長さ,面積を計算し表示します。 1辺の長さaが1の正三角形 高さ h: 面積 S:Ⅰ 面積の公式 以前の記事で、正三角形から正六角形までの面積の求め方を紹介しました。(「正多角形の面積の公式」を参照) 今回は、正 \(~n~\) 角形の面積、つまり一般化してみたいと



名師課輔網 求正三角形面積
S formula (1) area S = √s(s−a)(s−b)(s−c) s= (abc) 2 T r i a n g l e b y H e r o n ′ s f o r m u l a ( 1) a r e a S = s ( s − a) ( s − b) ( s − c) s = ( a b c) 2 お客様の声 アンケート投稿 よくある質問正三角形の面積を入力し「正三角形を計算」ボタンをクリックすると、入力された面積から1辺の長さ、高さを計算し表示します。 面積 S: 面積Sが1の正三角形〔考え方〕 展開図で考えたとき、 左の図の ae が求める長さです。 ① obe は30°,60°,90°の直角三角形 be は正三角形 obc のoc を底辺にしたときの高さ にあたるので,∠obe =30°,∠beo=90°です。
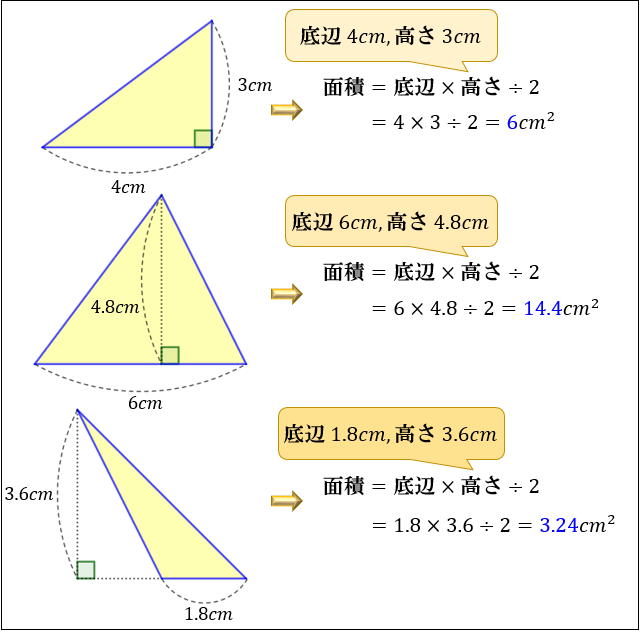
が、先生方でもなかなか作ることはできなかった。 2.3枚なら正三角形ができるよ 「折り紙で正三角形を作ろう」 と子どもたちに呼びかける。 子どもたちはまず折り紙を対角 線で折り(写真②)、「正三角形が できた!」とする。「おっ、できた《三角形の面積の求め方》 三角形の面積=底辺×高さ÷2であることから 答え 28㎠ 問題③ 次の三角形の面積を求めましょう。 《三角形の面積の求め方》 問題①・②と比べると三角形の形が傾いていますが、この三角形の面積を求める際に使う底辺は10cm。面積のもとめ方の工夫B 解説 面積のもとめ方の工夫c 解説 面積のもとめ方の工夫d 解説 まわりの長さ 解説 面積の求め方(ブロック地図) 解説 面積の求め方(ブロック図形) 解説 角とその大きさ 分度器 解説 分度器ペンつき 解説 分度器角度扇
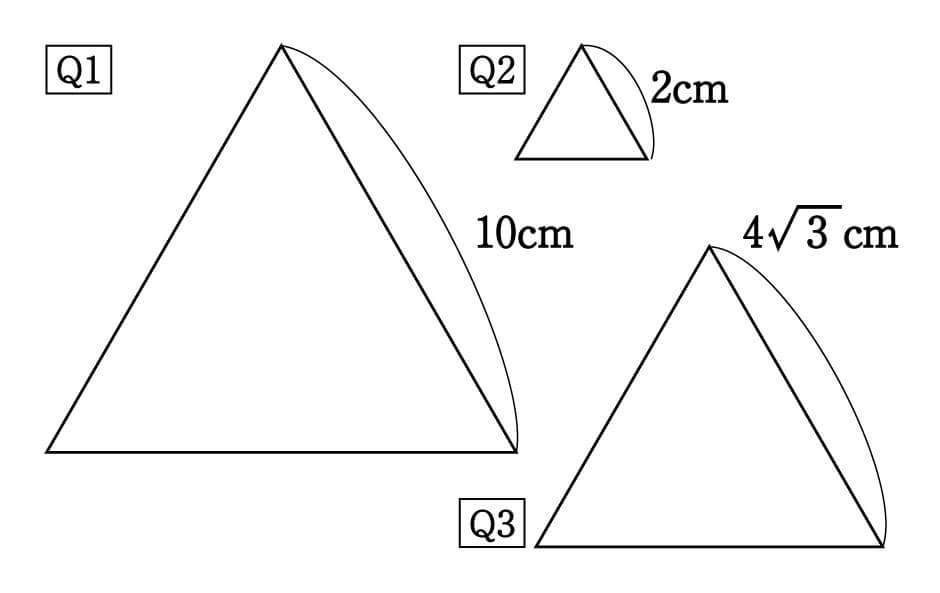
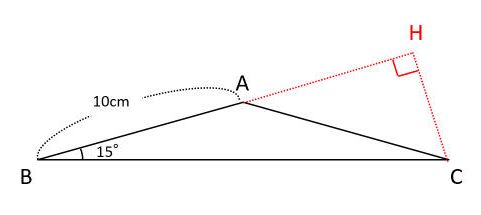
ABCの面積は? 答えその1 〈図a〉をあてはめて、正方形cbde を作ると、 aedは正三角形。 点aよりceの延長上に垂線afを 下ろす。 afeは30°の直角三角形 2 答えその2 下図のように正三角形cbd を作ると、 adbは底角15°の 二等辺三角形より、 ad=4なので正三角形の面積を利用することはできません。 円周率 求め方 多 角形 5 % 432 541 3 666 947 784 748 631 776 745 602 574 665 571 924 813 568 670 381 381 381 円周率(えんしゅうりつ、英 Pi 、独 Kreiszahl )とは、円の円周の長さの、円の直径に対する比率のこと で円とおうぎ形⑺ 正三角形が関係する問題 6 6 次の図は、1辺の長さが6㎝の正三角形と半円を組み合わせた図形です。 色のついた部分の面積を求めなさい。ただし円周率は314とします。 補助線を引いて、図形を2回移動させます。
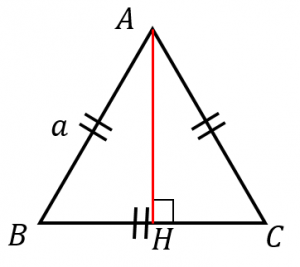



正三角形の面積の求め方 小学生用 高校生用 具体例で学ぶ数学
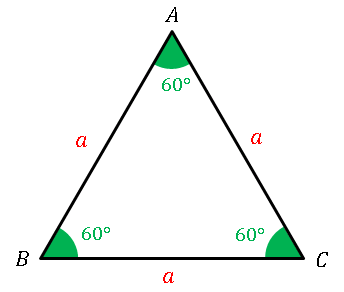



正三角形の性質 角度 面積 周の長さ 対称性
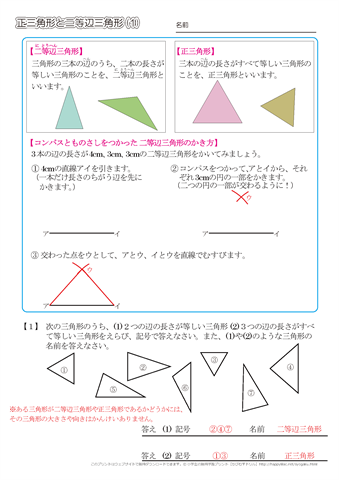
折り紙で正三角形を作る 今からやる方法でなぜ正三角形になるかは、後で中2の数学の範囲を使って証明します。 まずはやり方から説明します。 1.折り紙を半分に折る 画像ではわかりやすいように折り目に赤線を引いています。簡単公式 正三角形の高さの求め方がわかる3ステップ Qikeru 学びを 簡単 正三角形の面積公式が一瞬で分かる 見やすい図で徹底解説 正三角形 辺から高さと面積 三角形の計算 計算サイト 三平方の定理 正三角形の高さ 面積を求める方法を解説 数スタ 三角4=2√3 (eはocの中点) de=od-oe=3-2=1 bedは∠e=90°の直角三角形なので、三平方の定理が使えます。




正三角形面積求め方小學生 三角形の面積の求め方まとめ タイプ別でわかる公式一 Thomblake




高校数学でよく使う三角形の面積公式まとめ おいしい数学
インダクタンス物語(5)インダクタンスの求め方 音声付き電気技術解説講座 公益社団法人 日本電気技術者協会 電磁誘導現象は電気のあるところであればどこにでも現れる現象である。 このシリーズは電磁誘導現象とその扱い方について解説する黒くぬった部分の面積を求めなさい。 → 解答 問題6 次の図のように、半径5cmの円の中に各頂点が円周と接する正方形があります。図の黒くぬった部分の面積を求めなさい。円周率は、314とします。 → 解答 問題7 一辺が16cmの正三角形があります。ナイス! https//detailchiebukuroyahoocojp/qa/question_detail/q 0 fried_turnip fried_turnip さん 10/1/22 1149 半径5メートルなら、 内接する正三角形の高さは、75メートル 底辺は、75×2÷√3 面積は、75×75×2÷√3÷2≒325平方メートル 補足 円の中心は内接する正三角形の高さを2:1に分割します。 正三角形の辺と高さの比は2:√3です。 ナイス!
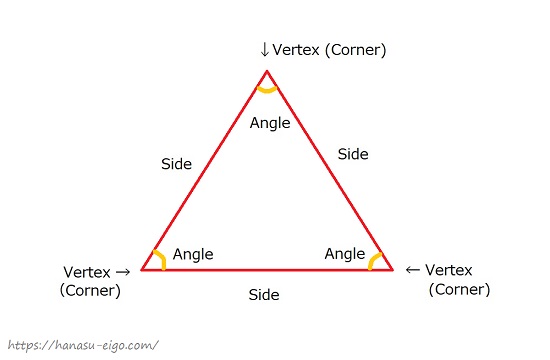



三角形 を英語で説明しよう 正三角形は 二等辺三角形は 話す英語 暮らす英語
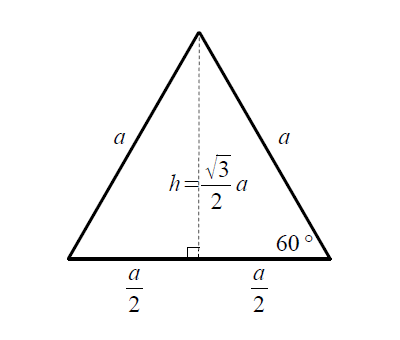



正三角形の面積計算 ゆるゆるプログラミング
正三角形 面積 求め方 小学生る.正三角形の大きさは一般の場合に設定してもよいが,計算しやすいように一辺の長さを2 としよう.面積 は p 3 になるので,正方形の一辺の長さは4 p 3 となることは容易にわかる.しかしこれだけわかっても一気に 正解に近づくわけではない.1辺の長さから正三角形の面積,周囲の長さ,高さを計算します。 辺の長さ a 6桁 10桁 14桁 18桁 22桁 26桁 30桁 34桁 38桁 42桁 46桁 50桁正十二角形の面積 正十二角形の面積の求め方を教えていただけ (東海中学 14年) 正三角形の作図と面積(麻布中学 07年) おうぎ形の角度と面積(14年 開成中学) 花火を見ることができるのは?(芝中学 14年) 台形



1



数学 正三角形の高さと面積は5秒で出せる 受験の秒殺テク 4 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
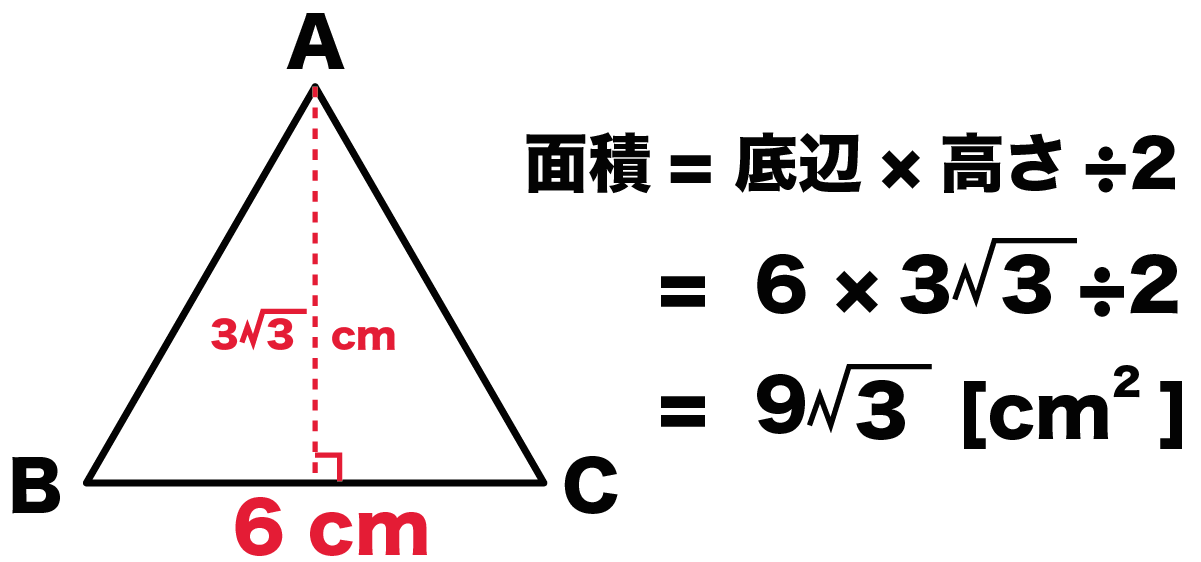
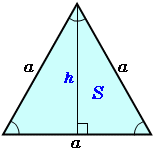
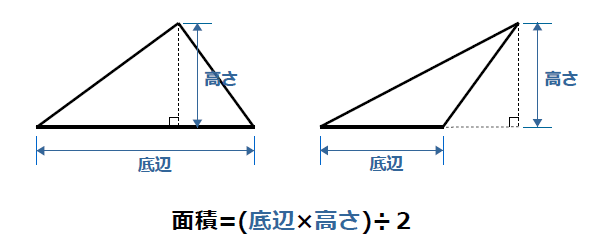
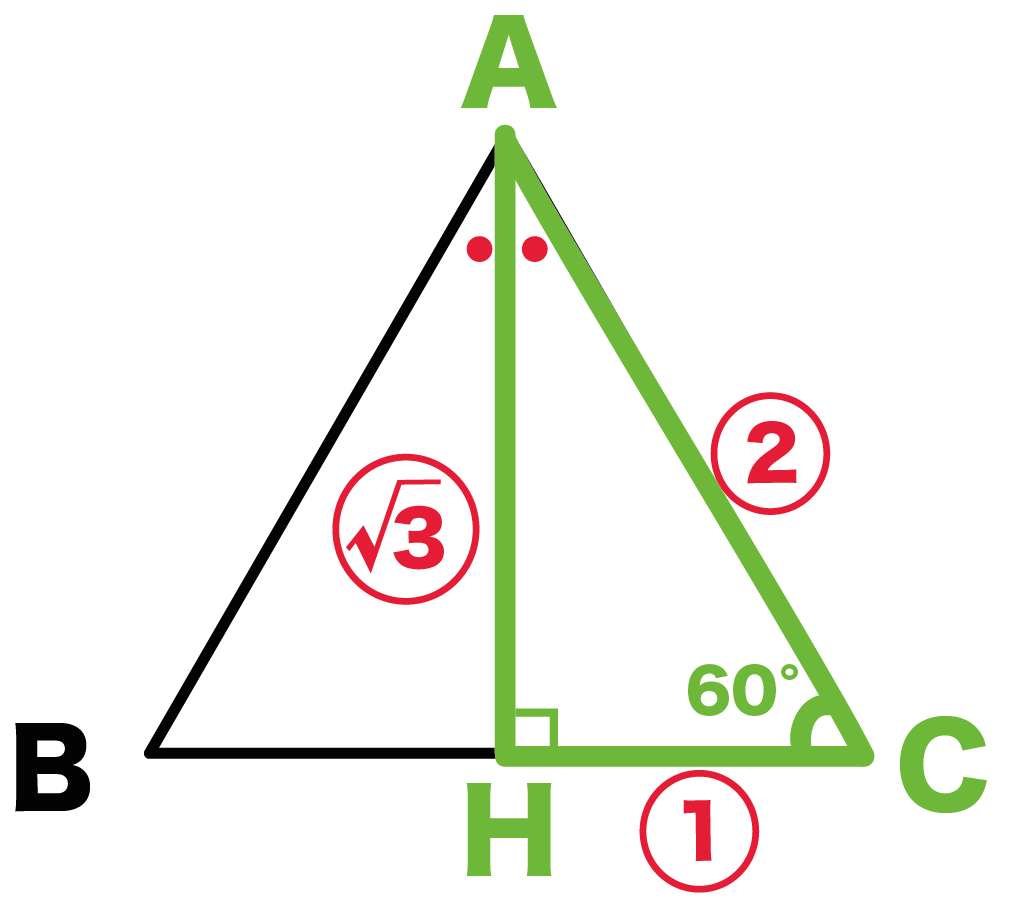
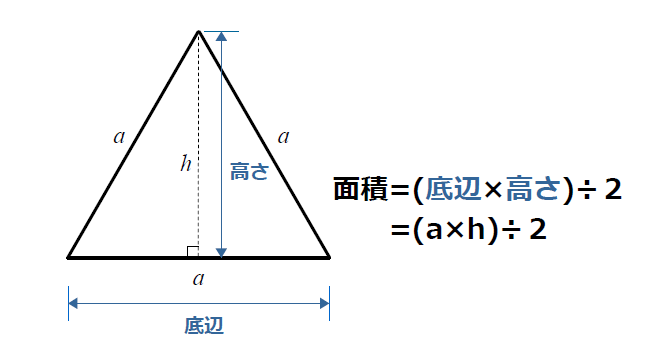
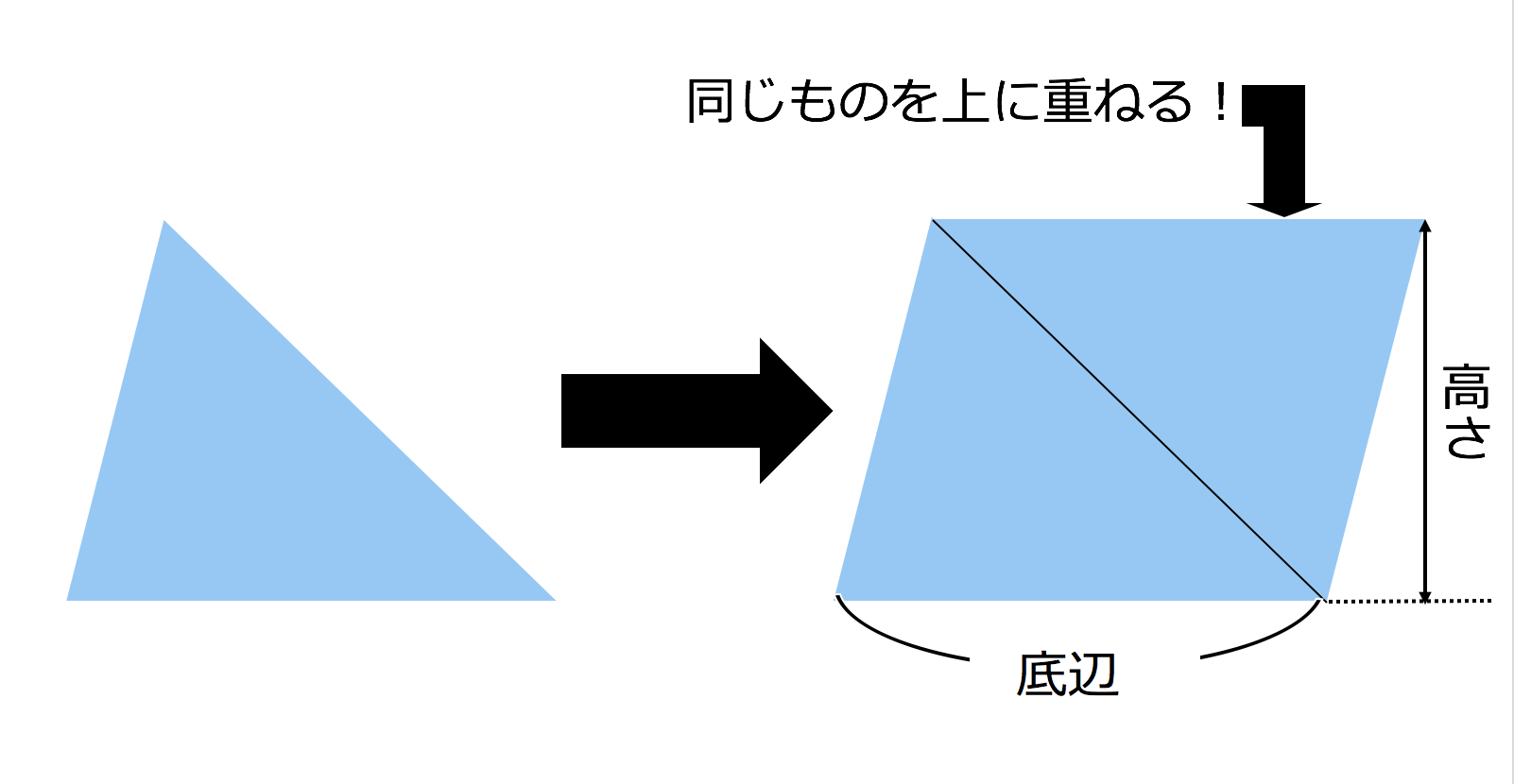
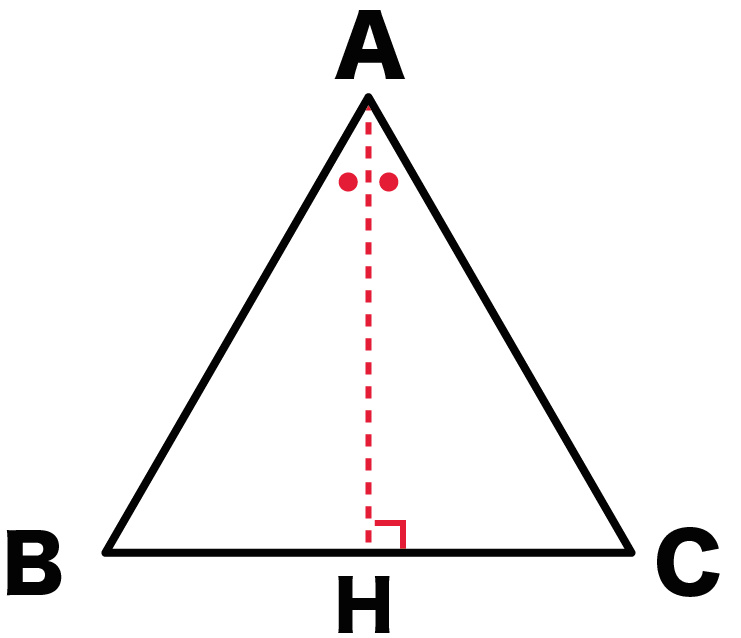
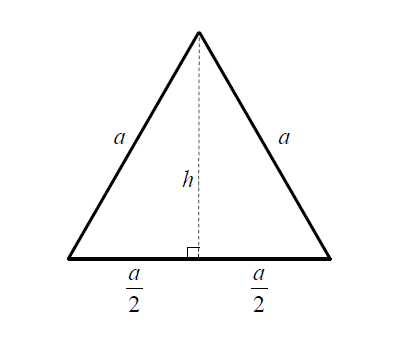
その正三角形の面積は、底辺×高さ÷2で求まります。 この高さですが、正三角形を頂点から底辺への垂線で 2つに分けると、合同な 直角三角形 が2つできます。正三角錐 底面が正三角形で,側面がすべて合同な二等辺三角形である 三角錐を,正三角錐という。 正三角錐の展開図は下のようになる。 注意 4つの面がすべて合同な正三角形であるときは,正四面体と いう。下の図は正四面体の展開図である。三角形の面積を求めるためには 一旦、平行四辺形の面積を求め それを半分にしている。 だから、2で割る必要があるんですね! 忘れないように覚えておきましょう(^^) 三角形の面積を求める問題 それでは、三角形の面積公式を使って問題を解いていきましょう。




数学 正三角形の高さと面積は5秒で出せる 受験の秒殺テク 4 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




最高 50 正三角形 面積 求め方
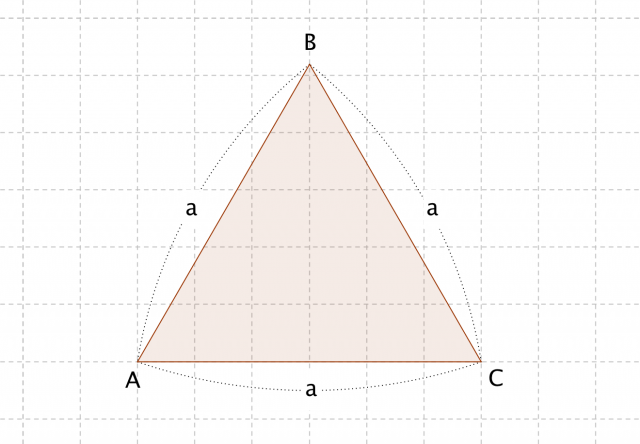
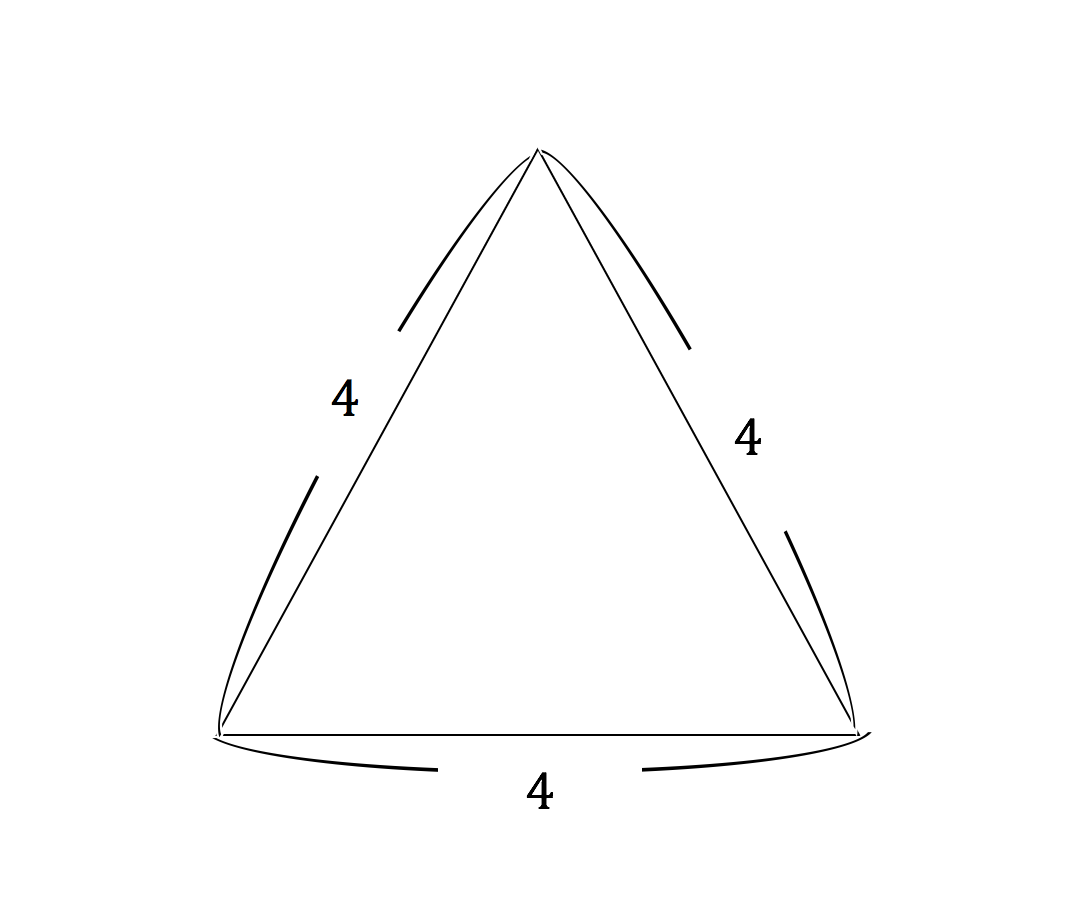
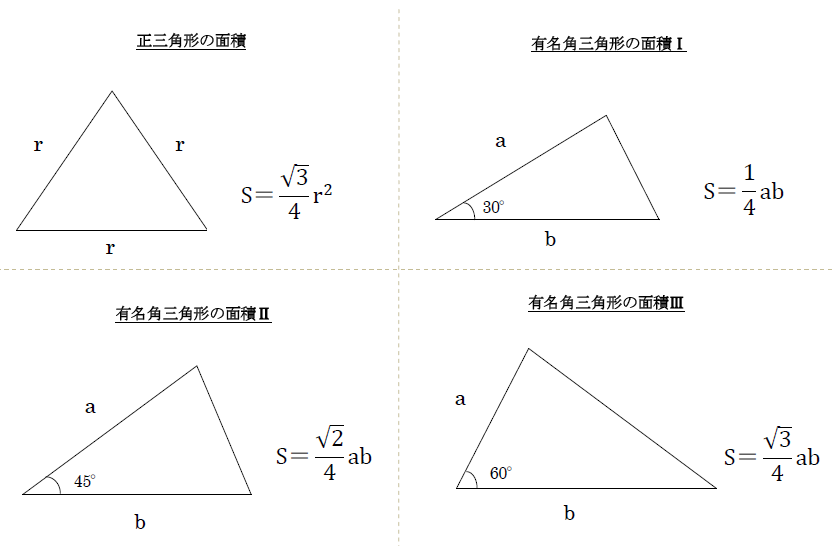
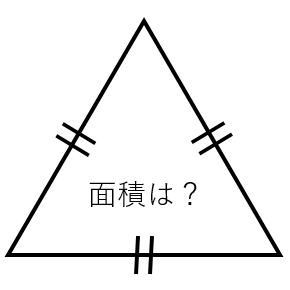
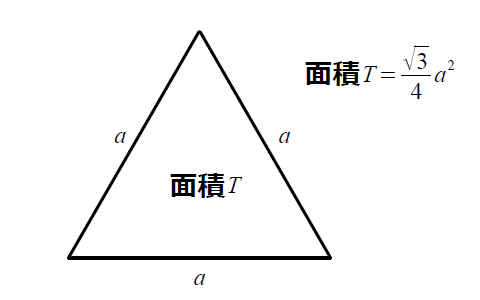
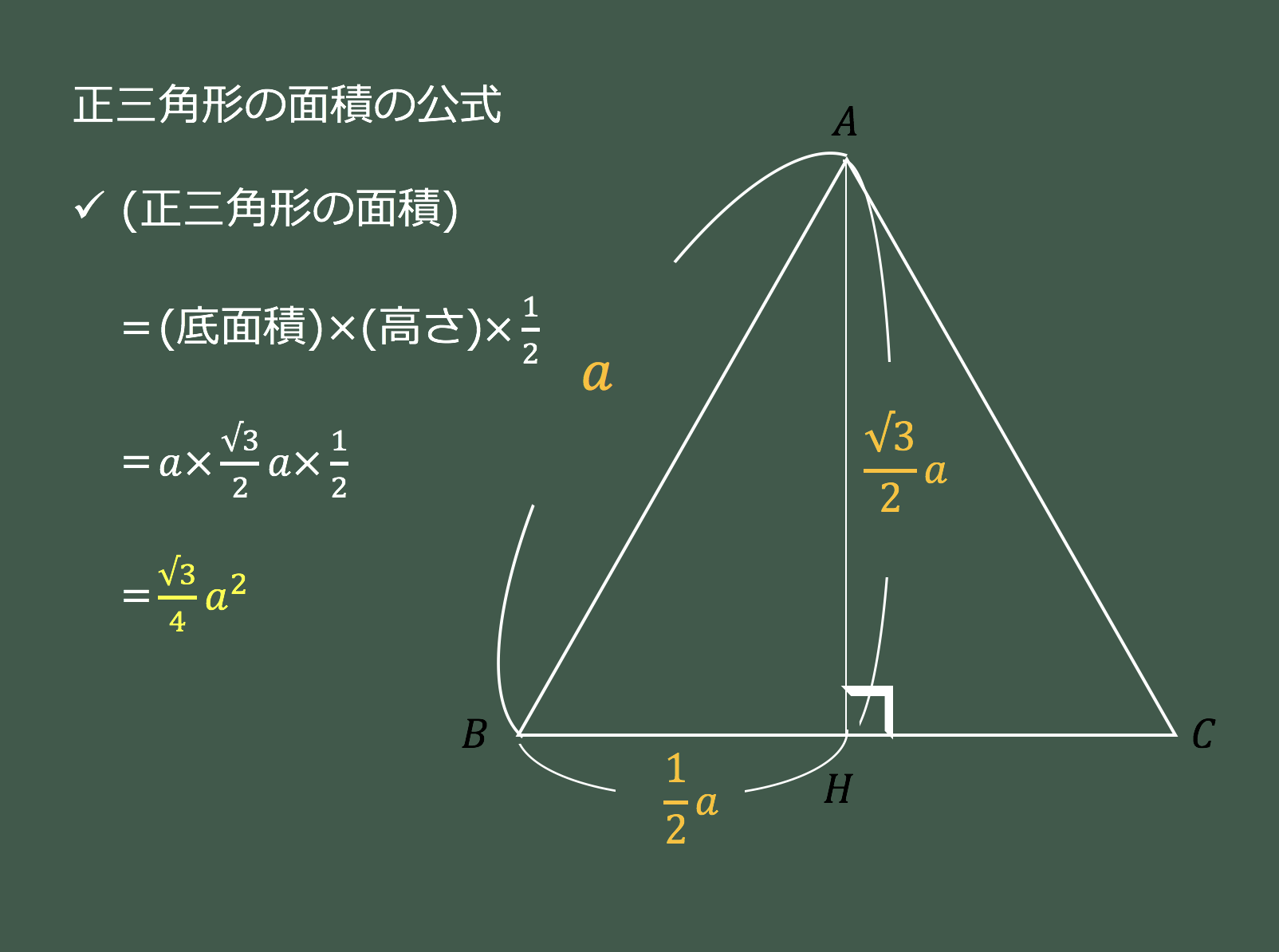
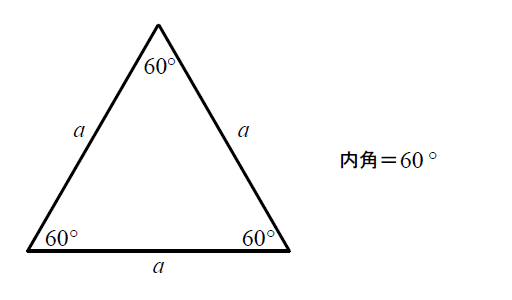
正三角形の面積の求め方 そもそも正三角形とは何かというと、 三角形の中で3つ全ての辺が等しいもの を言います。 それを押さえた上で解説を進めます。 上の図のような一辺の長さ の正三角形を考えてみましょう。 三角形の面積の求め方は (底辺)×さて、実際に正四面体の体積を求めます。 ここでは、先ほど説明した 正四面体の高さ を用います。 一辺 の正四面体の体積 一辺 の正三角形の面積 底面積 高さ となります。 正三角形の面積について復習したい方はこちらも参照してください。 3分で正三角形の面積には公式がある 。 便利でイカすヤツだ。 1辺の長さをaとすると面積は、 √3/4 a^2 になるんだ。 つまり、 (正三角形の1辺)×(正三角形の1辺)×



簡単公式 正三角形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




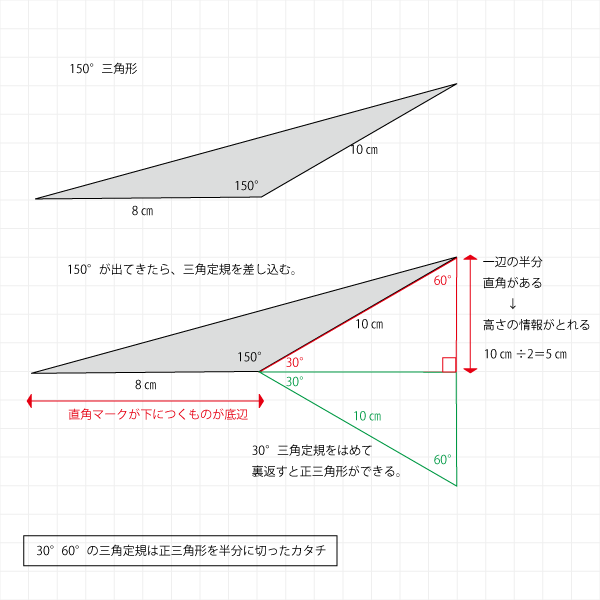
二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ
計算式 辺の長さをaとすると 正三角形の面積 (S) S = 3 4 a 2 正三角形の高さ (h) h = 3 2 a √3 = で計算しています。正多角形の内角の求め方 を解説していくよ。 よかったら参考にしてみてね^^ 4秒で計算できる! 正多角形の内角の公式 正多角形の1つの内角の大きさを求めたいときは、 つぎの公式をつかってみて。 正n角形の1つの内角は、三角形の面積は「 底辺 高さ 底 辺 ×
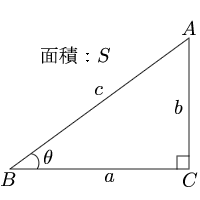



直角三角形 底辺と斜辺 三角形の計算 計算サイト



四角形に内接する正三角形の図形の面積問題 条件が三角形の一辺が Yahoo 知恵袋
簡単公式 正三角形の面積の求め方がわかる3ステップ Qikeru 学びを 正三角形の面積の求め方 小学生用 高校生用 具体例で学ぶ数学 簡単 正三角形の面積公式が一瞬で分かる 見やすい図で徹三平方の定理/特殊な直角三角形辺の比/正三角形・正六角形/その他/ 三平方と相似長さの計算 /直角三角形の2 つの鋭角に注目/ 面積の計算:高さが共通・底辺比→面積比/ 面積の計算:その他/辺の比→相似の証明/複素数 正三角形 1214 複素数で正三角形の頂点を求めたら、60°回転のとき、60°回転のときで、答えが逆になりました。 問題は 複素数平面上の3点z1=35i,z2=13i,z3=1i をそれぞれP,Q,Rとするとき、次の点を表す複素数を求めよ。 (2)正三角形PQTの頂点T




小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生




小5 面積 三角形の面積の求め方 日本語版 Youtube
一辺 (いっぺん) の長さ $a$ の三角形の面積 $S$ は、次の公式で求められます。 正三角形 (せいさんかくけい) の面積 \begin{align*} S = \frac{\sqrt{3}}{4} a^2 \end{align*} 面積 = 一辺 (いっぺん) ×CはBDの中点、EはFDの中点なので 中点連結定理より BF//CE①だということがわかります。 ①よりGF//CE②も言えますね。 そうすると ②より AGFと ACEは相似であるとわかります。 よってAG:GC=AF:FE=1:1③ ③よりGはACの中点であるとわかりました。 一度理解しておけば、あとは当たり前のように



三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典



正三角形の辺の比率は 1分でわかる値と計算方法 底辺と高さの比



3




直角二等辺三角形の面積を求める公式は 覚えずに自分でつくろう




サイン Sin を使って三角形の面積を求める練習問題一覧 数学i By ふぇるまー マナペディア
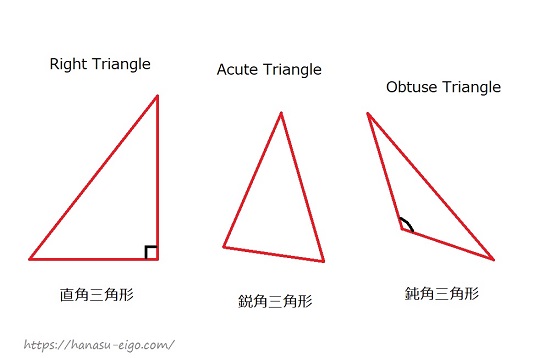



三角形 を英語で説明しよう 正三角形は 二等辺三角形は 話す英語 暮らす英語



C言語入門 正三角形の面積を計算 Webkaru



正三角形の面積 高精度計算サイト




高校数学 3辺 三角形の面積 を求める方法 映像授業のtry It トライイット
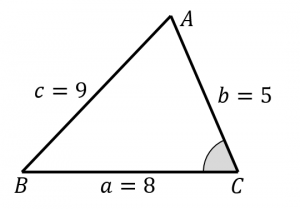



三角形の面積を3辺の長さから求める2つの方法 具体例で学ぶ数学
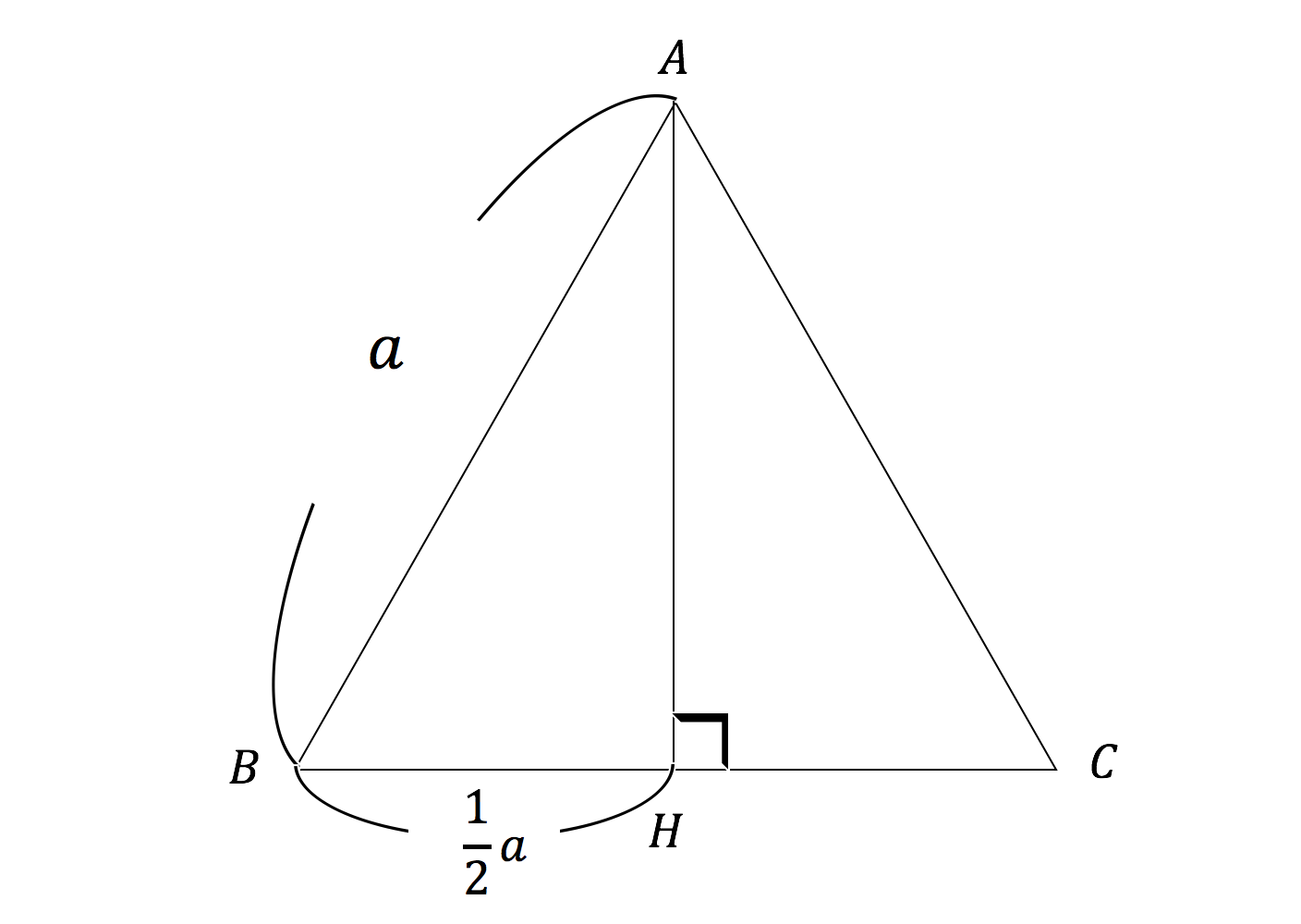



3分で分かる 正三角形の面積の求め方 公式をわかりやすく 合格サプリ



3分で分かる 正三角形の面積の求め方 公式をわかりやすく 合格サプリ



1



正三角形の高さの求め方は 1分でわかる計算 面積の求め方 二等辺三角形の高さの求め方




正三角形 直角三角形 の韓国語は 三角形の種類や特徴を表現してみよう 気になるkorean




高校数学b 三角形の面積のベクトル表示 成分表示とその証明 受験の月



簡単公式 正三角形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




数学の基礎 知ってる人は5秒で解ける正三角形の面積 Youtube




面積が 3cm の正三角形の1辺の長さは Cmである という問題について質 中学校 教えて Goo



三角形の面積計算 ゆるゆるプログラミング




図形note 正三角形の回転移動 受験算数に挑戦



受験 定期試験 数学解き方集 裏技 解法 三角形の面積 中学 高校




小5 算数 小5 42 三角形の面積 Youtube



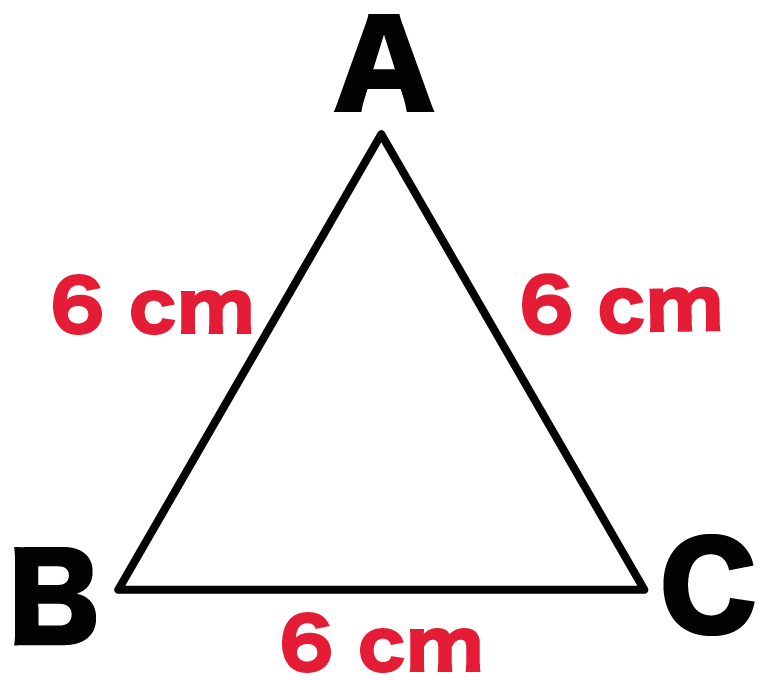
一辺の長さが6cmの正三角形の面積を求めなさいというのが分かりません Yahoo 知恵袋



半径5mの円の中にある正三角形の面積の求め方を教えて下さい 自分で求めた答え Yahoo 知恵袋




正三角形や二等辺三角形の内角 Youtube
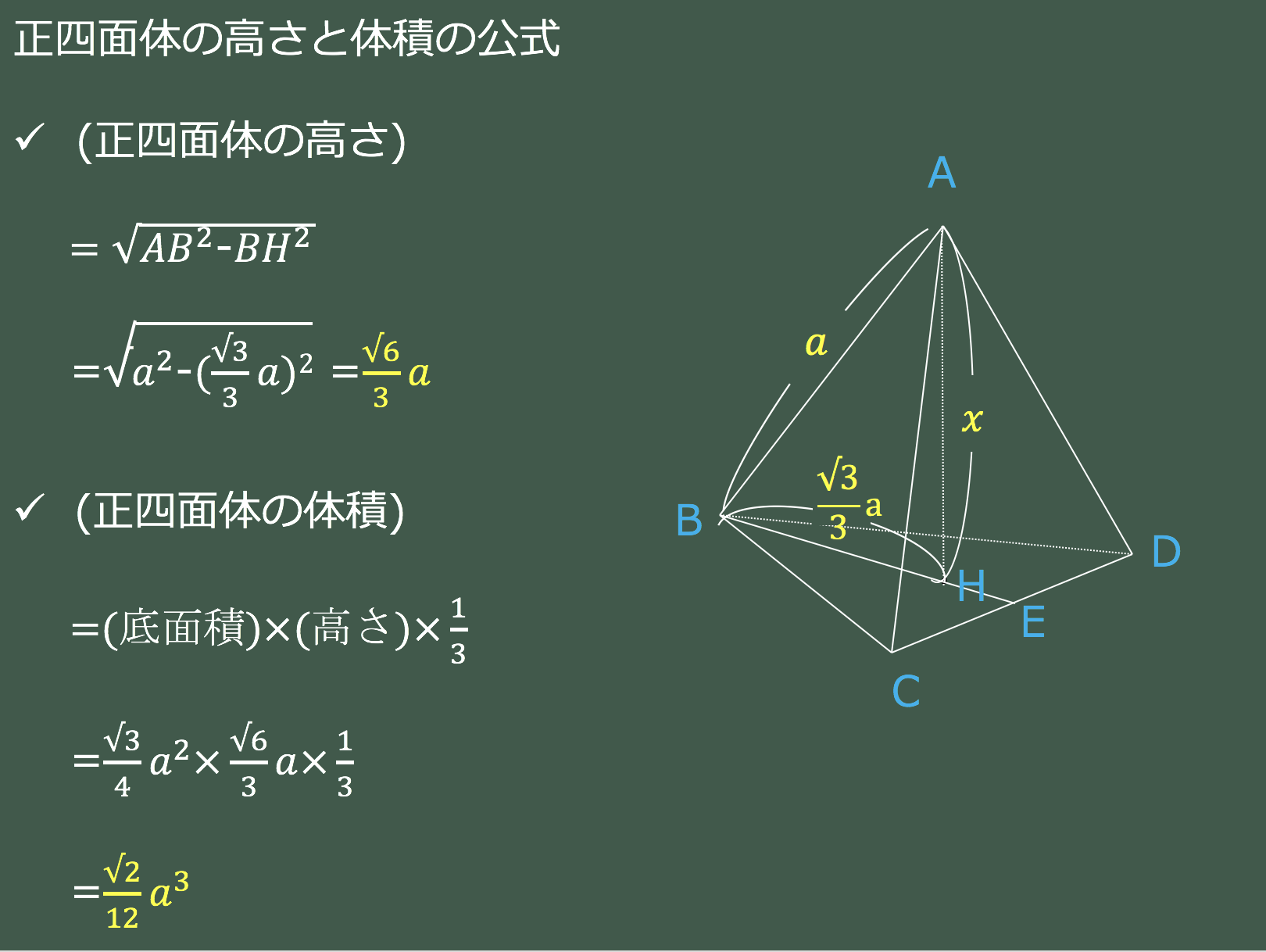



3分で分かる 正四面体の高さ 体積の求め方をわかりやすく 合格サプリ



正三角形 面積から辺と高さ 三角形の計算 計算サイト




円に内接する正三角形の問題 社会人になり勉強することもなくなったのですが Okwave




平面図形の苦手を解消 三角形の面積比 基本編
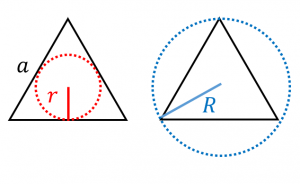



正三角形の内接円の半径と外接円の半径 具体例で学ぶ数学
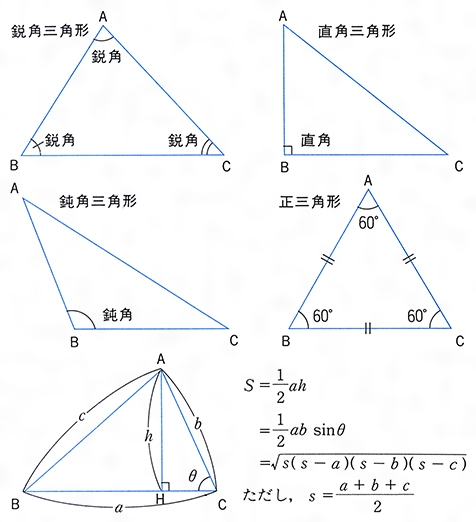



三角形とは コトバンク




斜線部の面積を求める 1 Youtube




正 三角形 面積



正三角形とは 定義や面積公式 高さや角度の求め方 受験辞典



名師課輔網 求正三角形面積



小学3年生の算数 三角形 正三角形や二等辺三角形 練習問題プリント ちびむすドリル 小学生




例題 正三角形的高與面積 Youtube




図形note 正三角形の回転移動 受験算数に挑戦




簡単公式 二等辺三角形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



簡単公式 正三角形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



1
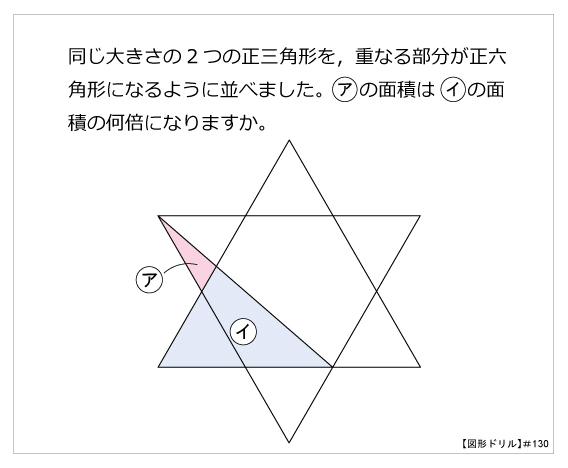



図形ドリル 第130問 正三角形を重ねた図形 算数星人のweb問題集 中学受験算数の問題に挑戦
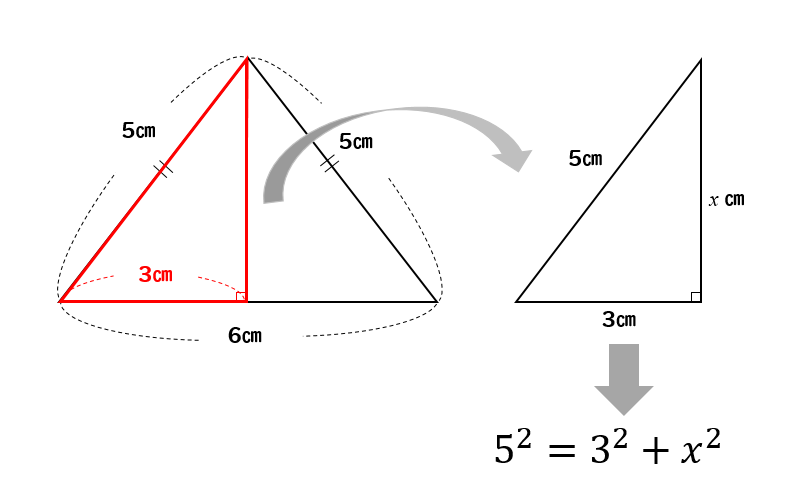



高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ



正三角形の面積の求め方 小学生用 高校生用 具体例で学ぶ数学



正三角形の面積計算 ゆるゆるプログラミング



一辺が8cmの正三角形の高さを求めなさい この問題が分かる方 教えてい Yahoo 知恵袋



正方形と正三角形が組み合わさった図形の面積計算 受験算数入門



正三角形の面積計算 ゆるゆるプログラミング




簡単公式 正三角形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




簡単 正三角形の面積公式が一瞬で分かる 見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ



相似の証明 2つの正三角形と共通な角 勉強ナビゲーター




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット



二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ
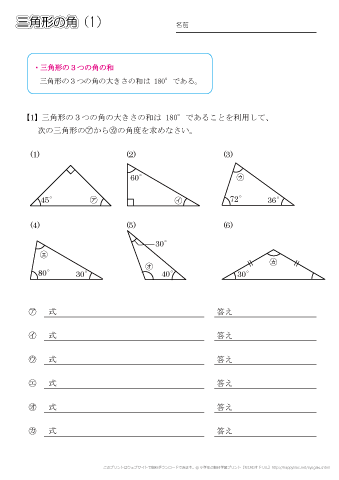



小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生




三平方06 正三角形の面積 Youtube




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ




高校数学 三角比 三角比を使った三角形の面積の求め方 Sin Cos ヘロンの公式を使った方法 数学の面白いこと 役に立つことをまとめたサイト



3分で分かる 正三角形の面積の求め方 公式をわかりやすく 合格サプリ




三平方の定理 ピタゴラスの定理 とは 応用問題パターンまとめ10選 遊ぶ数学



正三角形の面積 高さ 辺の長さの計算機 公式を使った求め方も紹介 やまでら くみこ のレシピ



正三角形と半円 灘中学 受験算数問題より どう解く 中学受験算数



3分で分かる 正三角形の面積の求め方 公式をわかりやすく 合格サプリ
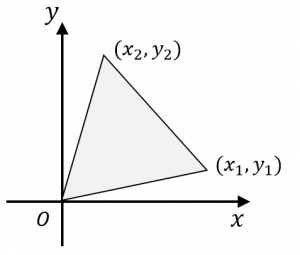



座標平面上で三角形の面積を計算する公式 具体例で学ぶ数学
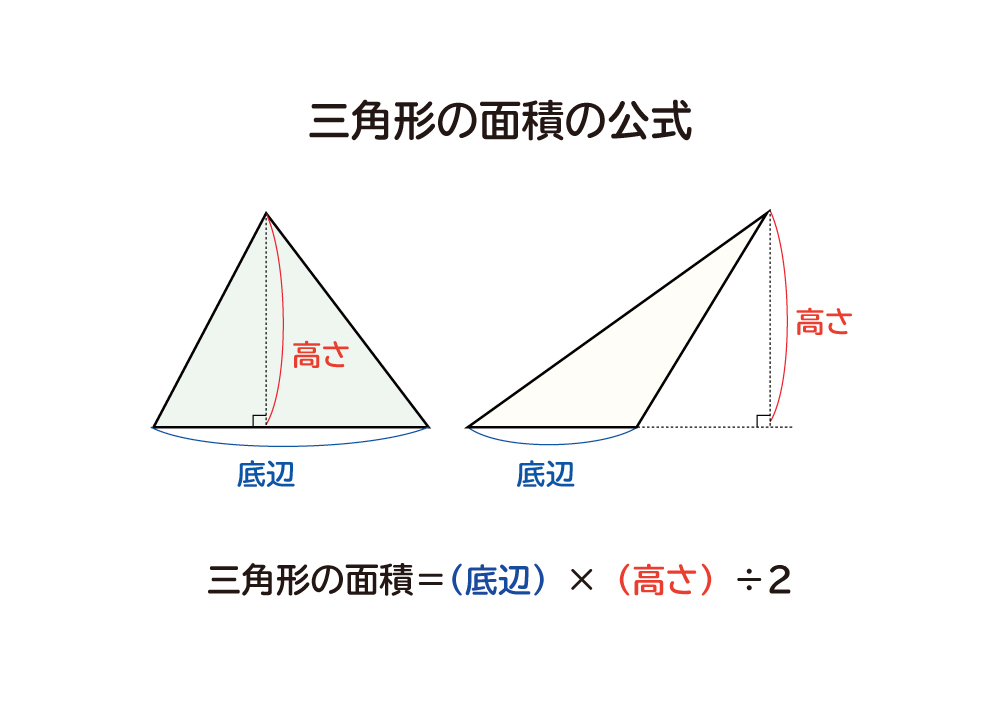



なぜ 三角形の面積は 底辺 高さ 2 なのか を説明します おかわりドリル




簡単公式 正三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト
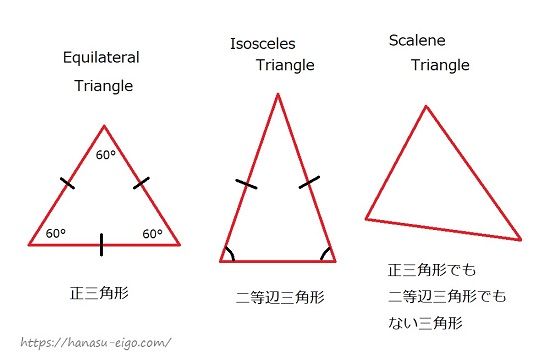



三角形 を英語で説明しよう 正三角形は 二等辺三角形は 話す英語 暮らす英語




面積の求め方を教えてください Clear




平面図形の苦手を解消 三角形の面積比 基本編
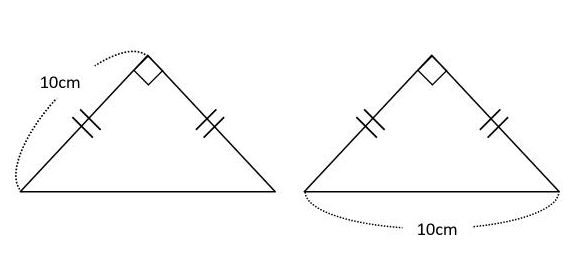



二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ




三角形の面積の公式 小学生に教えるための分かりやすい解説 数学fun




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ



正三角形 ゆるゆるプログラミング




3分で分かる 正三角形の面積の求め方 公式をわかりやすく 合格サプリ




面積の求め方 計算公式一覧




三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ
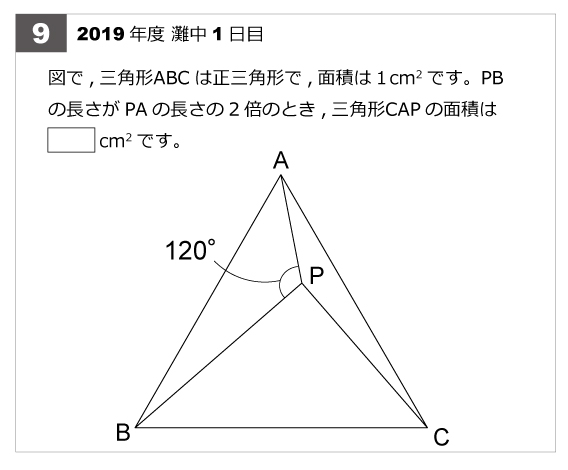



灘中解説速報 19年第9問 正三角形と面積比 算数星人のweb問題集 中学受験算数の問題に挑戦




ヘロンの公式で三角形の面積を求める 三辺の長さがわかっているときはコレ 数学の面白いこと 役に立つことをまとめたサイト



簡単公式 正三角形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




三平方の定理 正三角形の面積を求める Youtube
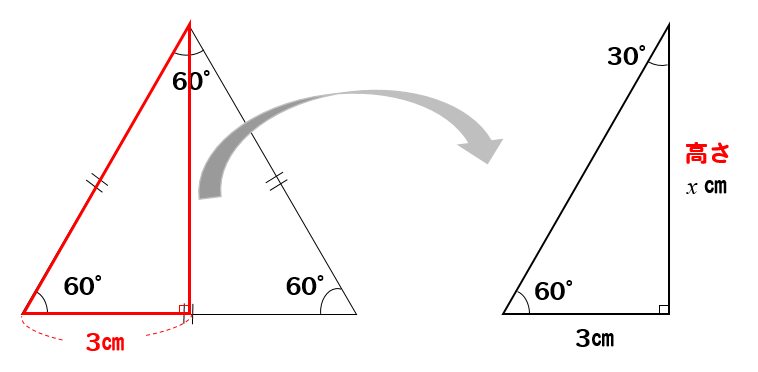



三平方の定理 正三角形の高さ 面積を求める方法を解説 数スタ



正三角形の面積計算 ゆるゆるプログラミング




中学数学が秒でわかる 正三角形の中に正三角形がある図形の証明 超 解説付き なぜか分かる はかせちゃんの怪しい研究室




平面図形をマスター 三角形の面積比 応用編その3




小学6年生で三角形の面積求め方わかりません 小学6年生の親です 学 数学 教えて Goo




三角形面積求め方 三角形とは 面積公式 角度 辺の長さ 重心 比の計 Jbqhd



三角形の面積の求め方 なぜ底辺 高さ 2で求まるのか アタリマエ



0 件のコメント:
コメントを投稿