数学Ⅱ(三角関数):sinθ の値 数学Ⅱ 対象 高2 再生時間 9 説明文・要約 ・角の範囲が 0≦θ<2π(0°≦θ<360°)に拡張されても、単位円の y座標が sinθ の値になる。 ・sinθ の値の範囲は -1≦sinθ≦1 (単位円上を行ったり来たりする關 鍵 字: 三角函數、函數與方程式及其圖形、扇形面積 授權資訊: 創用cc 姓名標示非商業性相同方式分享 25 台灣 作者: 旭聯科技 (數位典藏與數位學習國家型科技計畫第六分項子二計畫) 作者: 陳燕靜 (市立成功國小) 提供者:ラジアン(英 radian, 記号 rad)は、国際単位系 (SI) における角度(平面角)の単位である。 円周上でその円の半径と同じ長さの弧を切り取る2本の半径が成す角の値と定義される。 弧度(こど)とも言い、平面角の大きさをラジアンで測ることを弧度法と呼ぶ。。あるいはラジアンで測った平面

扇形面積公式推導 編程樂其中 數學不好 看你怎麼編 每日頭條
扇形面積 公式 弧度法
扇形面積 公式 弧度法-半径がa(cm 2)で中心角が45°の扇形の面積S(cm 2)は 例題2 右図のように半径a(cm)の円とこれにに外接する正方形(1辺の長さは2a(cm))で囲まれた斜線部の面積は弧度法で扇の弧の長さと面積を求める公式 弧度法を使って、扇の弧の長さと面積を求める公式を紹介します。 半径がr、中心角がθの扇の弧の長さをl、面積をSとするとき ※θは、度数法ではなく弧度法



扇形面积计算圆扇形弧形计算公式谁有计算圆弧长扇形面积和圆锥的面积的公式 尚书坊
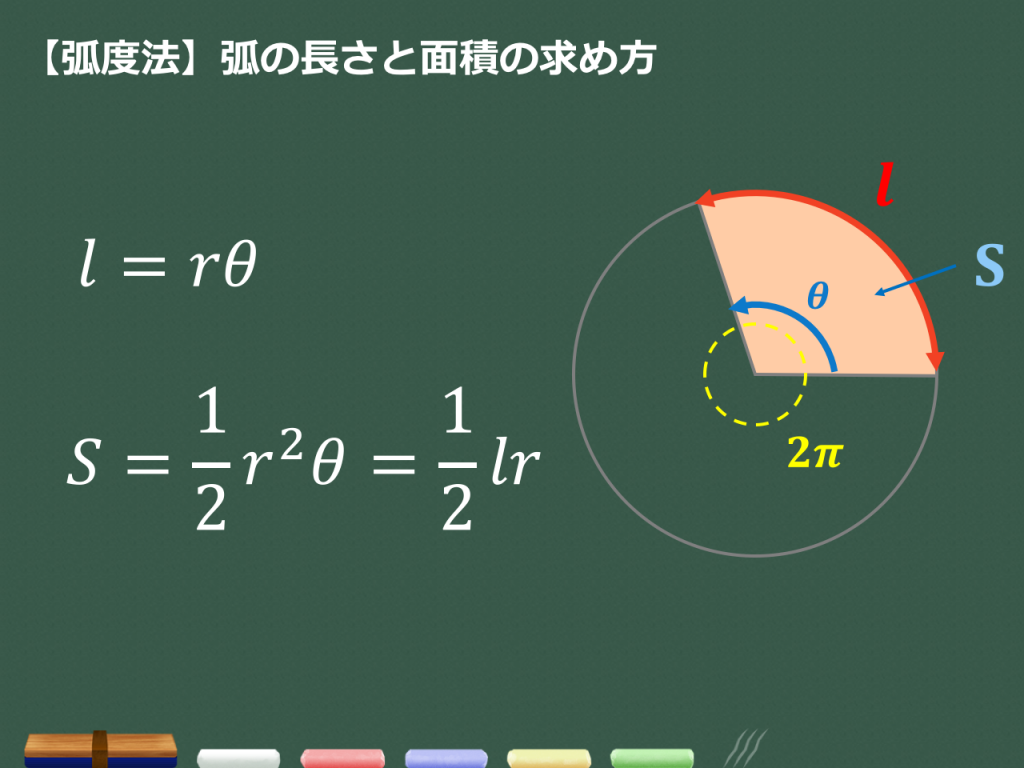
弧度法における面積公式 半径 r r r ,中心角 θ \theta θ ラジアンの扇型の面積は 1 2 r 2 θ \dfrac{1}{2}r^2\theta 2 1 r 2 θ 例えば,半径が 2 2 2 で中心角が π 4 \dfrac{\pi}{4} 4 π ラジアンである扇形の面積は, 1 2 × 2 2 × π 4 = π 2 \dfrac{1}{2}\times 2^2\times\dfrac{\pi}{4}=\dfrac{\pi}{2} 2 1 × 2 2 × 4 π = 2 π と計算できます。数学Ⅱ 第4章 三角関数 第4章 三角関数1.一般角と弧度法 角度を360°より大きい角や,負の角にまで拡張します.これは一般角と呼ばれています. そののち,これまで慣れ親しんだ度数法という角度の表し方とは異なる,弧度法という新しい角度の表し方を導入します.弧度法は,これ以降の角の単位の中心となります. この節の最後に,扇形の弧の長さと面積さて、弧度法を使うことにより何が変わるかというと、例えば、扇形の弧の長さや 面積を求める式が以下のように変わります。 半径 r 、中心角d°=θ rad の扇形について、
扇形の面積を求める公式は、次の通りです。 S = πr2 × x 360 = 1 2lr S = π r 2 × x 360 = 1 2 l r 中心角 x°、半径 r の扇形 ここで、S は扇形の面積、π は円周率、r は円の半径、x は中心角(単位「度」)を以上、三角関数の微分の公式を"説明しました"。実は、上の説明は、完全に厳密な"証 明"ではありません。どこが問題かというと、上の"説明"の中で (i) 半径1の円の面積はπ である。 (ii) 扇形の面積は、中心角に比例する。 の2点を使っているところ性質。除扇形面積公式。 sIV15 認識線與線、線與平面在空間中的垂直 關係和平行關係。不調整 sIV16 理解簡單的立體圖形及其三視圖與平面 展開圖,並能計算立體圖形的表面積、側面積及 6 理解平面圖形相似的意義,知道圖形 經縮放後其圖形相似,並能應
一、弧度與扇形周長與面積 (1)弧度制: (a)弧度量的定義: 設有一圓,圓心為O,半徑為r。在圓周上取一段圓弧 ∩ PQ ,使得圓弧 ∩ PQ 的 長度等於r,規定這一段圓弧 ∩ PQ 所對的圓心角∠POQ就定義成1 弧度。 (b)度與弧度之互換:6n12 能理解圓面積與圓周長的公式,並計算簡單扇形面積。 6s04 能理解圓面積與圓周長的公式,並計算簡單扇形面積。 6a05 能用中文簡記式表示圓面積、圓周長與柱體的體積公式。 觀念學習一 圓的周長 例題: 半徑為5公尺的圓,圓周長是多少公尺?扇形旋風 胡哲瑋 杜昭宜 蔡瑞寶 發展分數、圓心角轉換的具體操作經驗,以利於扇形面積公式的理解 v ii_s_12 b0422 長得像的圖形 (二) 侯雪卿 圖形的放大與縮小 v ii_n_16 b0423 水果新樂園 阮正誼 整數的非整數倍 v ii_n_17 b0424 搶數字大戰 韋秀麗




扇形面積公式推導 編程樂其中 數學不好 看你怎麼編 每日頭條



初中数学 求阴影部分面积 如何计算不规则扇形面积呢 哔哩哔哩 つロ干杯 Bilibili
扇形の面積の公式:円弧×半径/2 に代入 もしくは、円全体の面積 πr 2 に割合 θ/2π を掛ければ求まる 関連動画一覧圓其扇形 Ocd 的面積, 則 A = r2 r1 B。 設扇形 Ocd 的夾角為 θ, 透過扇形面積公式 1 2 r2 1θ, 則可 得 A = r2 r1 B = 1 2 r1r2θ, 由這個式子可以很容易瞭解整個橢圓面積為 r1r2π (考慮 θ = 2π)。 此時整個解題關鍵在於如何計算θ, 假設c 點座標為 (c1,c2), d 點座標為 (d1,d2), O 為 もしおうぎ形ではなく円であれば、面積は πr2 π r 2 なので、比で考えると S πr2 = θ 2π S π r 2 = θ 2 π なので、これを S S について解くと S = 1 2r2θ S = 1 2 r 2 θ となります。 もちろんこれでもいいのですが、弧の長さの式を使ってさらに変形することもできます。 弧の長さを l l とすると、 l = rθ l = r θ なので、 S = 1 2rl S = 1 2 r l となります。 この式変形は単純です



已知扇形的面积为2 扇形圆心角的弧度数是4 则扇形的周长为 高中一年级 数学试题 弧度制 弧度与角度的互化考点 好技网



Q Tbn And9gcr6gw9fhpzovmfob2ngp9u Gvimmrq94zqc64t Ysfbxqs9wsbi Usqp Cau
ラジアン (rad) とは?定義 ラジアン (\(\mathrm{rad}\)) とは、角の大きさを表す単位の \(1\) つです。 円の半径と同じ長さの弧を切り取るときの角の大きさ が「\(\color{red}{1 \ \mathrm{rad}}\)」と規定されます。 孤の長さを基準に考えることから、ラジアンは「孤度」とも呼ばれ、ラジアンによって角扇形,I,醐半臥 単軌 円周率×ミ宗 を学ぶが,これが 弧の長さ = 半径×中心角の弧度 扇形の面稚 = 半径×半径×中心角の弧度T2 = 半径×弧の長さT2 となる特に扇形の面紗よ三角形の面積とr同じ」 と見なせることがわかる 二のこと1つをとっても弧度の図形的な扱い扇形の面積 面積も弧の長さと同様に比例式を使います。 扇形の面積も中心角の大きさに比例するので,半径\(r\)の円の面積は\(\pi r^{2}\),中心角\(2\pi\)なので
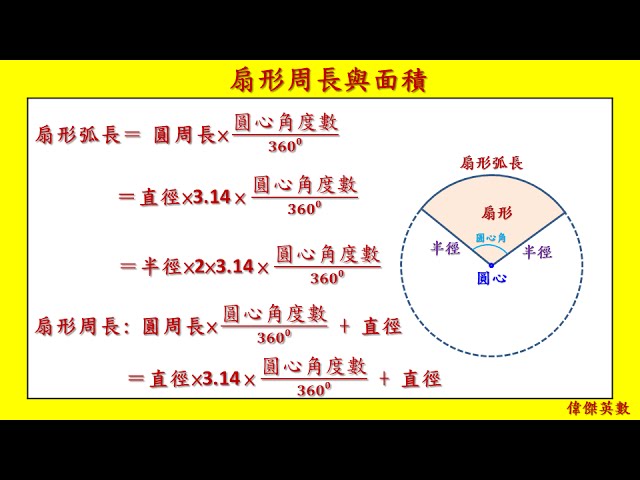



扇形周長與面積 6年級數學 Grade 6 Math Fan Shaped Area Youtube




扇形弧長 扇形弧長是扇形的兩條半徑之間的圓弧長度 一條圓弧和經過這條圓弧 百科知識中文網
8 圓與扇形的面積 81 圓面積 1122 圓與扇形的面積 扇形面積 1122 圓與扇形的面積 解題 1122 圓與扇形的面積 9 規律問題 91 間隔問題 2505 間隔問題 92 找規則 2506 找規則 10 等量公理 101 認識等量公理 2511 認識等量公理 102 加與減的等量 $$扇形の弧の長さ=直径 \times 円周率\times \frac{中心角}{360}$$ 円の面積 円の面積と円周の公式はどっちがどっちだか わからなくなることがありますのでしっかり確実に覚えておくようにしましょう。 円の面積 = 半径 × 半径 × 円周率 弧の面積 扇形の面積も弧度法で この流れで扇形の面積も求めてみましょう。やることは同じでまず度で考えます。 先程と同じように半径が \(r\) の扇形を考えて中心角を \(\alpha\) 度としましょう。
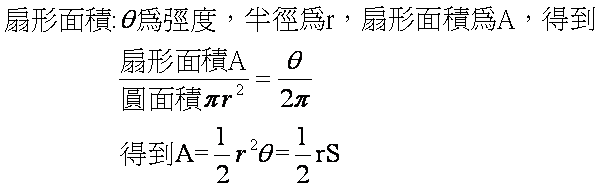



扇形的弧長與面積
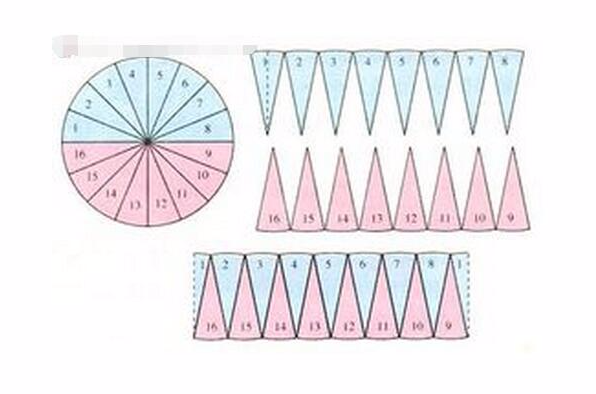



圓面積公式 圓形面積 來源故事 扇形 公式推導 圓面積公式 圓周長公式 中文百科全書
扇形の弧の長さと面積を,弧度法をもちいて表してみよう. 図のように半径が r ,中心角が θ の扇形の弧の長さを l ,面積を S とすると,弧度法の定義より θ = l r だから ∴ l = r θ (1) 面積と中心角の比から S θ = π r 2 2 π ∴ S = 1 2 r 2 θ (2) 以上, (1) , (2 小学扇形面积公式:S扇形=(nπR的平方)/360 其中 n表示扇形圆心角的度数,派表示圆周率,R表示半径。 因为圆形为360度,扇形就是N度角的圆形,所以: 1、n度圆形(扇形)面积为: 2、n度圆形(扇形)所对应的弧长为: ,所以, ,带入表达式中, 即扇形面积为扇形の面積の求め方を教えてください! (2 図1 の容器を展開すると, 下の図3 のような, 中心角が1' のおうき形になりました。 このおうぎ形の面積を求めぶさい。




扇形的弧長公式 Youtube




扇形面積公式弧長14 Zilhc
扇形面积公式是:s=lr/2 公式说明:s是面积,l为扇形弧长,r为半径,α为弧度制下的扇形圆心角。 若命扇形的顶角(扇形的弧所对的圆心角,叫做扇形的顶角)为a,那么 其中 (1)式适用于六十分制。 (2)式适用于百分制。 (3)式适用于径制(弧度制)。01 圓周 Circumference 雖然學生在小學階段已學習過圓周公式,但根據經驗很多學生並不能回憶起公式。此課件可將圓周攤開,讓學生直觀地認識圓周約為直徑的三倍。教師可細分刻度及放大圖像,引導學生明白圓周為直徑的Pi倍。高中選修數學乙(上) 21 弧度、弧長 2 (1) s=rθ。 (2) A= 1 2 r2θ= 1 2 rs。 2 特別注意,在使用這兩個公式時,θ 都要先化為弧度。 例題2 求扇形的弧長與面積 由一圓弧與一弦所圍成的區域稱為弓形。



圆的周长与面积 弧长 扇形的面积 玄数




九年級數學 弧長及扇形的面積 知識點
中心角がθである扇形の弧の長さl、面積Sを求めるための公式は以下の通りです。 半径rの円の円周の長さは2πr、面積は\(πr^2\)であるのは既に習いましたよね。 扇形の弧の長さや、面積は中心角に比例します。 そのため扇形の円周の長さや面積は 弧度法x radの中にπのニュアンスが含まれているので扇形の弧や長さの公式にπは現れません。 例題:次のものを求めよ。 (1) 半径3,中心角1radの扇形の弧の長さ (2) 半径5,中心角04radの扇形の面積 (3) 中心角05rad,弧の長さ4の扇形の面積6n12能理解圓面積與周長公式並計算簡單扇形面積。 6a01能理解等量公理。 6a02能使用未知數符號,將具體情境中的問題列成兩步驟的算式題,並嘗試解題及驗算其解。 6a04能在比例的情境或幾何公式中,透過列表的方式認識變數。
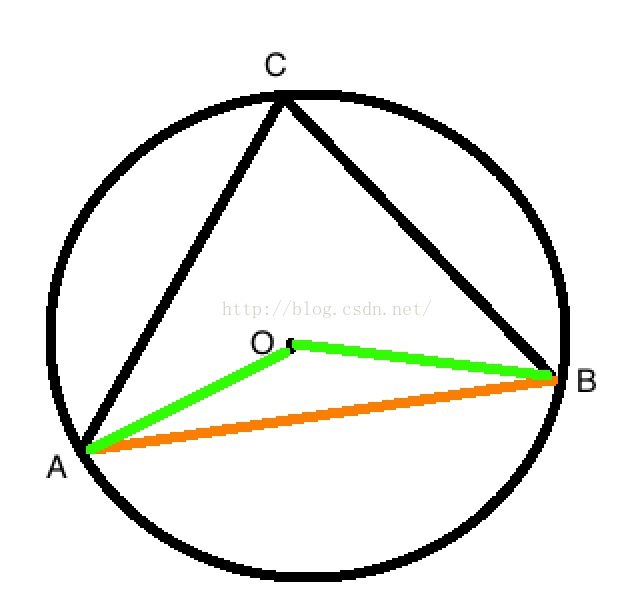



圆周角 圆心角 弦 弦心距 弧长 扇形面积 打鱼还是晒网 Stone 程序员宅基地 程序员宅基地




圓的周長與面積 16 扇形弧長計算的練習 Youtube
前回 https//googl/zBDZJZ 次回 https//googl/iSWs6k動画のプリント(19ch) http//www19chtv/サブチャンネル とある男が扇形の面積 弓形の面積(中心角から) 弓形の面積(弓形の半径と高さから) 弓形の面積(弓形の弦長と高さから) 楕円の面積 楕円扇形の面積 楕円弓形の面積 放物線の弓形 双曲線弓形の面積 双曲線扇形の面積 地図をなぞって面積を計算三角形の面積(3辺からヘロンの公式) 三角形の面積(1辺と2角から) 正方形の面積 長方形の面積 台形の面積 台形の高さ・面積(4辺の長さから) 台形の1辺・面積(3辺の長さと高さから) ひし形の面積 平行四辺形の面積(底辺と高さから)



扇形面积公式推导图 万图壁纸网



扇形面积计算圆扇形弧形计算公式谁有计算圆弧长扇形面积和圆锥的面积的公式 尚书坊
弧度法で弧の長さと面積をだす公式が腑に落ちません弧の長さは、半径 x 中心角(ラジアン)面積は、半径 x この長さ x 1/2とのことですが、なぜ上記の公式で、弧の長さと、面積を求めることができるのでしょうか?π:円周率中心角面積(英語: Area )是用作表示一個曲面或平面 圖形所佔範圍的量,可看成是長度(一維度量)及體積(三維度量)的二維類比。 對三維立體圖形而言,圖形的邊界的面積稱為表面積。 計算各基本平面圖形面積及基本立體圖形的表面積公式早已為古希臘及古中國 人所熟知。扇形面積公式 web 數學∕面積∕正方形 web 延伸閱讀 數學 討論數量、形狀及它們之間的關係的科學。包括算術、代數、幾何、三角、解析幾何、微分、積分等。




小學數學弓形面積怎麼求 每日頭條



题型 2弧长与扇形面积公式的计算 哔哩哔哩 つロ干杯 Bilibili
055~ 扇形の弧の長さ506~ 扇形の面積719~ 練習問題一夜漬け高校数学~一夜漬けでの小さな努力で大きな成果を出すためのいくつかの提案 扇形の面積 = 弧の長さ × 半径 ÷ 2 なんとなく、三角形の面積と同じように面積を求めることができてしまうのです。では、どうしてこのようなことがいえるかを考えて見ましょう。 扇形の面積を求める公式は前に述べたとおり以下の公式です。 今回は扇形(おうぎ形)の面積・弧の長さ・まわりの長さの求め方について書いていきたいと思います。 扇形(おうぎ形)の面積の求め方 扇形の弧の長さの求め方 扇形のまわりの長さの求め方 扇形の面積・まわりの長さを求める問題 問題① 《扇形の面積の求め方》 《扇形のまわりの長さの



扇形面积公式大全 搜狗图片搜索




初中數學 圓的性質 扇形面積公式及應用 異常重要 每日頭條
扇の面積 続いて扇の面積について考えてみましょう。 円の面積はr×r×πで求められました。 先ほどと同じように考えます。 2πの角度のときにその面積はr×r×πです。 では角度がθのときはどうなるでしょうか。 2π:r×r×π=θ:S これを整理すると ②(ただしθは弧度法で表したものに限る) また弧度法と角度の公式 弧度法による角度の公式は下記です。 θ=L/r θは角度で単位はラジアン、Lは円弧の長さ、rは半径です。円弧の長さ、半径も単位は同じです。よって無次元数となり単位は省略することが多いです。便宜的にradを付けることもあります。 角度が度数法で与えられた場合、扇形の面積を求める公式は次のとおりです。 扇形の面積の公式度数法 半径が \(r\)、中心角が \(\theta\) \(({}^\circ)\) の扇形の面積 \(S\) は



扇形面积怎么求 扇形面积怎么计算 尚书坊



扇形面积计算公式图解 万图壁纸网



扇形面积的计算公式 扇形面积的计算公式画法



扇形面积计算圆扇形弧形计算公式谁有计算圆弧长扇形面积和圆锥的面积的公式 尚书坊



Q Tbn And9gctoaftep Cp0mxb1byahotggx3ub73wafwbkzah7fg7xmsh2anr Usqp Cau



高中数学必修四 基础详细讲义附答案38页 小初高题库试卷课件教案网



扇形面积计算圆扇形弧形计算公式谁有计算圆弧长扇形面积和圆锥的面积的公式 尚书坊



扇形面积计算圆扇形弧形计算公式谁有计算圆弧长扇形面积和圆锥的面积的公式 尚书坊
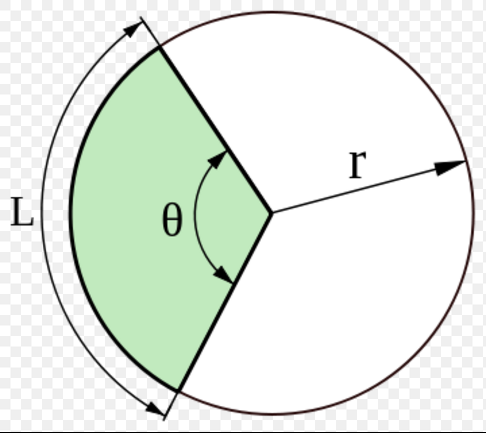



扇形 簡介 組成部分 面積 弧長 周長 其他知識 中文百科全書



扇形面积的计算公式 扇形面积的计算公式画法



扇形面积的计算公式 扇形面积的计算公式画法



弧度制 扇形弧长公式 面积公式 数学作业 解题作业帮




Ppt 弧度制powerpoint Presentation Free Download Id




上扇形面積公式弧度 扇形面積公式弧度法



扇形弧长公式 扇形弧长公式画法



扇形面积的计算公式 扇形面积的计算公式画法



扇形弧长公式 扇形弧长公式画法



使用数学中的微积分推导出扇形的的面积公式a 1 28r 2 哔哩哔哩 Bilibili



扇形弧长的两个公式 西瓜视频搜索



扇形面積題庫面積和體積 二 Jkveno




扇形面積公式弧長14 Zilhc



扇形面积的计算公式 扇形面积的计算公式画法




圓的周長與面積 15 如何計算扇形的弧長 Youtube




高中數學必修四 三角函數突破點 二 弧度制及其應用 每日頭條



圆的周长与面积 弧长 扇形的面积 玄数



功課幫



扇形面积公式推导图 万图壁纸网



扇形面积公式 弧长公式与扇形面积公式 尚书坊




扇形平台钢格板怎么计算弧长和扇形面积 安平润潭金属网业www Runtanwangye Com



弧形的面积公式 西瓜视频搜索



扇形面积弧长公式 扇形面积公式高中 扇形面积弧长公式弧度制




扇形面積公式弧長14 Zilhc



扇形面积的计算公式 扇形面积的计算公式画法



扇形的面积公式 哔哩哔哩 つロ干杯 Bilibili



扇形面积的计算公式 扇形面积的计算公式画法



扇形面积的计算公式 扇形面积的计算公式画法



Pizyjhxhyp7aum



扇形面積計算公式第二章三角函數 rbmi




数 你好看 任意角三角函数与诱导公式 知乎
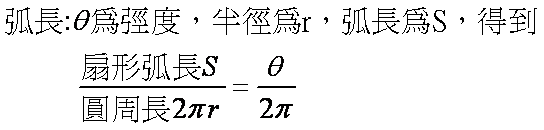



扇形的弧長與面積




高中數學 三角函數 數乙 弧長與扇形面積公式ii 曾政清 Youtube



Q Tbn And9gcqpqxxknzceay3mjcxzcklaz Iozcfat84mkqdgzflcwlamy23 Usqp Cau



腾讯视频



扇形面积公式大全 搜狗图片搜索



扇形面积计算 万图壁纸网




九年級數學 弧長及扇形的面積 知識點
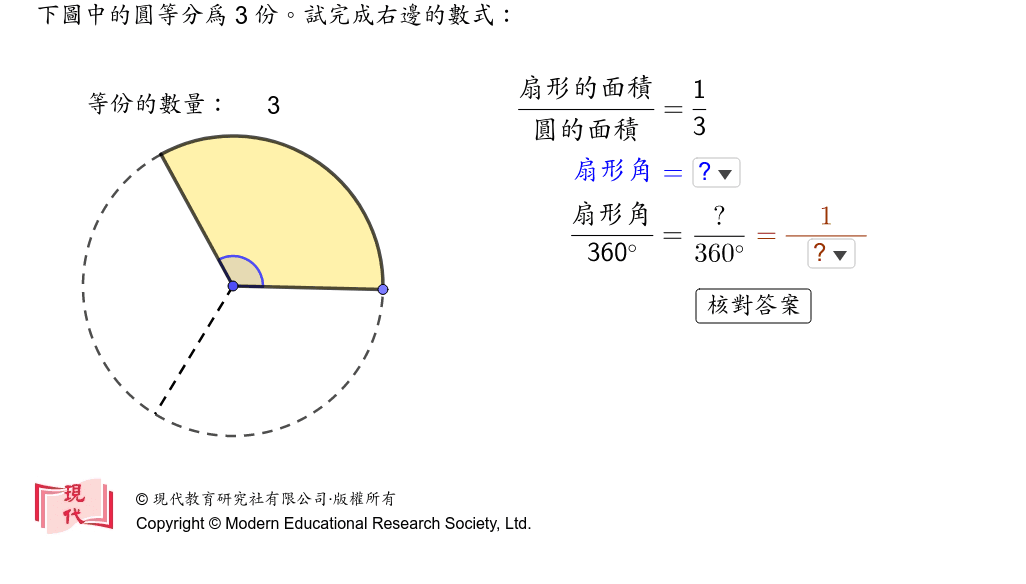



扇形面積公式 Geogebra



扇形面积的计算公式 扇形面积的计算公式画法



弧度转角度翻译



扇形面积计算 万图壁纸网



扇形弧长自拍 公式与弧长公式高中v扇形扇形 高中课题目




高中數學必修 一題多解 三角函數 扇形的面積求法 每日頭條




弧度計算弧長計算公式 弧長公式 N是圓心角度數 R是半徑 L是圓心角弧長 Aypsaf



上扇形面積公式弧度 扇形面積公式弧度法



扇形弧长公式 扇形弧长公式画法




基礎 給扇形面積求圓心角 Youtube



扇形面积计算 万图壁纸网




扇形的弧長與面積




高校数学 一般角と弧度法 扇形の弧長l R8と面積s 1 2r 8 受験の月




高中數學必修四 三角函數突破點 二 弧度制及其應用 每日頭條



Http Www Hkedcity Net Res Data Edbltr Math 1001 00 742ed36a32ee4caaed Unit 4 C Pdf



1



高中数学扇形弧长公式 西瓜视频搜索




例題 如何計算扇形的弧長 數學 均一教育平台




数学 弧度法と扇形 さくらの個別指導 さくら教育研究所 Skredu



扇形弧长的两个公式 西瓜视频搜索



扇形面积的计算公式 扇形面积的计算公式画法




圓面積公式的介紹by Cp Ma




中考數學圓中弧長及扇形的面積計算專題 1 每日頭條




高中數學必修四 三角函數突破點 二 弧度制及其應用 每日頭條




001 弧度 弧長及扇形面積原理 Youtube




圆周长计算公式




2 圓心角所對弦長 弧長與扇形面積 基本觀念 國三上2 2 Live數學學習網 Www Liveism Com 名師葛倫 Youtube




扇形面积公式汉字 扇形的面积公式 三人行教育网 Www 3rxing Org




面積 40 由圓心角來求扇形大小 Youtube



扇形面积怎么求 扇形面积怎么计算 尚书坊



扇形面积的计算公式 扇形面积的计算公式画法



三角函数弧长和扇形面积公式 哔哩哔哩 つロ干杯 Bilibili




扇形面積公式弧長14 Zilhc



3 9 弧长及扇形的面积 哔哩哔哩 つロ干杯 Bilibili




圓面積公式 圓面積公式是圓周率 半徑的平方 用字母可以表示為 S Pr 華人百科



扇形面积的计算公式 扇形面积的计算公式画法



扇形的弦长计算公式 西瓜视频搜索



扇形面积扇形面积 面积公式 爱华网



0 件のコメント:
コメントを投稿